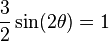Last week I wrote about rehearsing a with violin exam candidate, and looking for the “meaning” of the piece (a Bach Adagio).
Well, funnily enough, a few days later I found myself going through the same piece of music with another candidate. He was also struggling to find any kind of understanding of the music. Now, he happens to be studying maths, and physics and all sorts of mathematical kinds of subjects, so I approached the problem differently. “Suppose it is a complex and beautiful mathematical proof, or maybe something to do with physics, which you can just about understand if you follow it very carefully – maybe something like this…”
An identity is a statement resembling an equation which is true for all possible values of the variable(s) it contains. Many identities are known, especially in trigonometry. Probably the best known example is: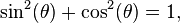 
, which is true for all values of θ.
In the process of solving an equation, it is often useful to combine it with an identity to produce an equation which is more easily soluble. For example, to solve the equation:
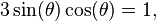where θ is known to be between zero and 45 degrees,
use the identity: 
so the above equation becomes:
Whence:
- I’ve just copied and pasted that lot from with Wikipedia page on equations. I’m not pretending that I actually understand what it says (although, as I did Maths with Music as my degree, there was a time when I might have known what it meant!)
- He thought about it, and then we played the piece again. I’m not sure what was going on in his head, but the music was now expressive, flowing, had a sense of journey and destination.
- I’ve done the same kind of thing with a Baroque allegro – Vivaldi, maybe. For one student, we talked about a surprise opportunity to go to Paris for fashion week, with all the catwalk shows, and staying in a top class hotel. For another student, playing the same piece, we discussed a culture trip to Venice, visiting churches, museums, art galleries and so on. It’s just a case of knowing what will inspire, connect, enthuse each student.
